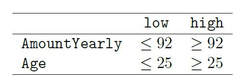|
This month's blog post was contributed by my colleague Susanne Berger. Thank you, Susanne, for the highly interesting read on attrition (churn) for committed givers and how to investigate it with methods and tools from data science. Johannes What this post is about The aim of this post is to gain some insights into the factors driving customer attrition with the aid of a stepwise modeling procedure:
The problem Service-based businesses in the profit as well as in the nonprofit sector are equally confronted with customer attrition (or customer churn). Customer attrition is when customers decide to terminate their commitment (i.e., regular donation), and finds expression in absent interactions and donations. However, any business whose revenue depends on a continued relationship with its customers should focus on this issue. We will try to gain some insights into customer attrition of a selected committed giving product from a fundraising NPO. Acquisition activities for the product took place for six years in total and ended some years ago. Essentially, we are concerned about how long a commitment lasts and what actions can be undertaken to prolong the survival time of commitments. We worked with a pool of some 50.000 observations. To be more specific, we are interested in whether commitments from individuals with a certain sociodemographic profile or other characteristics tend to survive longer. Survival analysis is a tool that helps us to answer these questions. However, it might be the case that the underlying decision process of an individual to terminate a commitment has different influence factors than the decision to start supporting. The approach chosen is to first ask whether an individual with one of the respective commitments has started paying, and if she has, we will have a look at the duration of the commitment. Both of these questions are depicted in a separate model:
The data Let's catch a first glimpse of the data. The variables ComValidFrom and ComValidUntil depict the start- and enddate of a commitment, ComValidDiff gives the length of a commitment in days, and censored shows whether a commitment has a valid enddate and is equal to one if the commitment has been terminated, and equal to zero if the commitment has not been terminated (until 2017-10-14). R Code - Snippet 1
Age and AmountYearly (the yearly amount payable) are, among others variables such as PaymentRhythm, Region and Gender included in the analysis, as they potentially affect the survival time of a commitment or the probability of an individual starting to donate. At the moment, no further explanatory variables are included in the analysis. The analysis After having briefly introduced the most important variables in our data, let's take a look at the results: Has an individual even begun to donate within the committed gift? First, we need to construct a binary variable, that allocates a FALSE if the lifetime sum of a commitment (variable ComLifetimeSum) is zero. Individuals who started to donate if the lifetime sum is larger than zero get assigned a TRUE. The variable DonorStart distinguishes between these two cases. R Code - Snippet 2
A popular way of modeling such binary responses is logistic regression, which is a mathematical model that can be employed to estimate the probability of an individual starting to donate, controlling for certain explanatory variables, as in our case Gender, Age, AmountYearly, PaymentRhythm, and Region. Thus, we fit an exemplary logistic regression model, assuming that Age and AmountYearly have a nonlinear effect on the propability to start paying. In addition, interactions of Age and Gender, as well as of Age and PaymentRhythm are included. For example, the presence of the first interaction effect indicates that the effect of Age on the probability to start to donate is different for male and female individuals. All estimated coeffcients are significant at least at the 5% significance level (except two of the Region coefficients and the main gender effect). R Code - Snippet 3
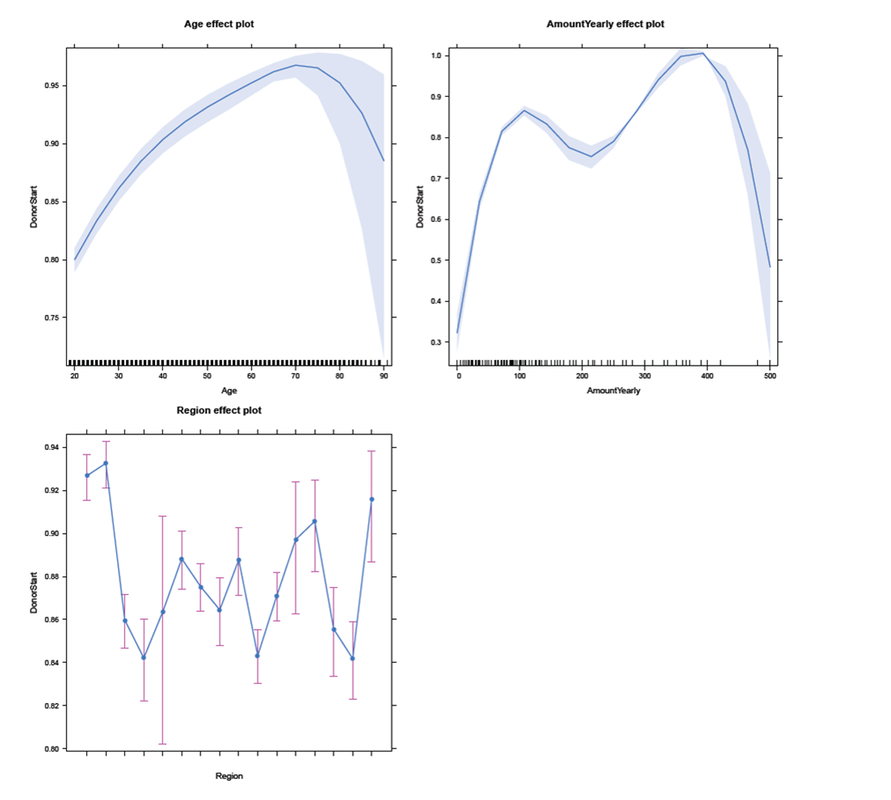
Usually, the results are presented in tables with a lot of information (as for example p-values, standard errors, and test statistics). Furthermore, the estimated coefficients are difficult to translate into an intuitive interpretation, as they are on a log-odds scale. For this reasons, the summary table of the model will not be presented here. An alternative way to show the results is to use some typical values of the explanatory variables to get predicted probabilities of whether an individual started to donate. An effects-plot (from the effects package) plots the results such that we can gain insights into how predicted probabilities change if we vary one explanatory variable while keeping the others constant. R Code - Snippet 4
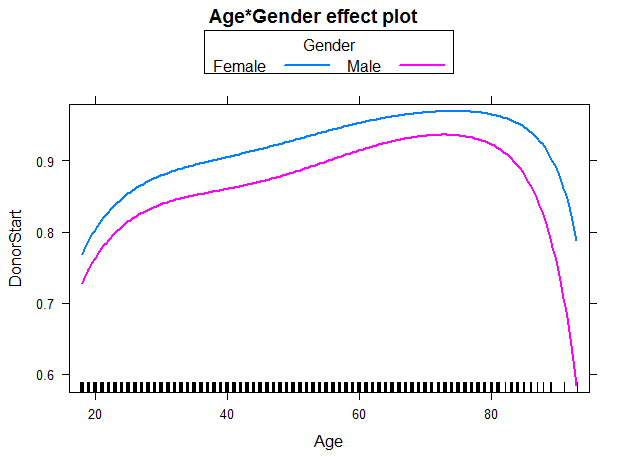
 In the subsequent panel, the effects plot for the interaction between Age and Gender is depicted. For all ages, females have a higher probability to start to donate than males. In addition, regardless of gender the older the individual (up to age 70-75), the higher the probability to start to donate. For individuals in their twenties, the steep slope indicates a larger change in probability for each additional year of age than for individuals older than approximately 30 years. We use the following code to create the effects plot: R Code - Snippet 5
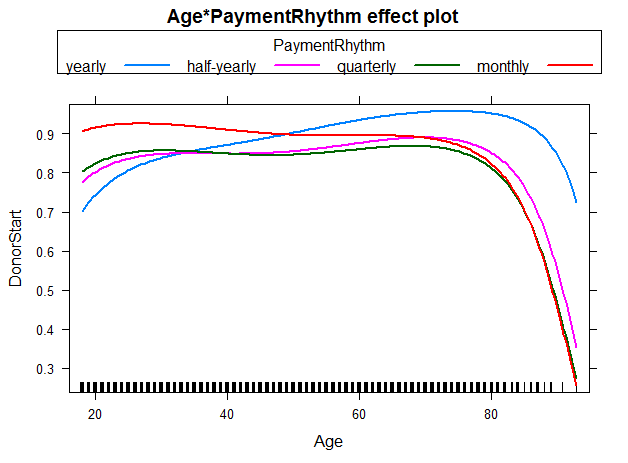
 We were also interested in the the interaction between Age and PaymentRhythm. As most of the individuals in the sampe decided for either yearly or half-yearly payment terms, one should not put too much confidence in the other two categories quarterly and monthly. Nevertheless, for individuals with a yearly payment rhythm, the probability to start to donate increases with age up to 70-75 years. For individuals with half-yearly or quarterly payment rhythm, rising age (up to 70-75 years) does not seem to affect the probability of starting to donor much. And for a monthly payment rhythm, the probability even seems to decrease slightly with rising age. The figure below illustrates these findings: R Code - Snippet 6
 Now, let's go one step further and try to investigate which factors have an influence on the duration of a commitment, once an individual has started to donate. The question we ask: What affects the duration of a commitment, given the individual acutally started paying for it? Survival analysis analyzes the time to an event, in our case the time until a commitment is terminated. First, we will have a look at a nonparametric Kaplan-Meier estimator, then continue with a semi-parametric Cox proportional hazards (PH) model. For the sake of brevity, we will neither go into the computational details, nor will we discuss model diagnostics and selection. To start the analysis, we first have to load the survival package and create a survival object. R Code - Snippet 7
The variable Survdays reflects the duration of commitments in days. The "+" sign after some observations indicates commitments that are still active (censored), and thus do not have a valid end date (ComValidUntil is set to 2017-10-14 for these cases, as the last valid end date is 2017-10-13): R Code - Snippet 8
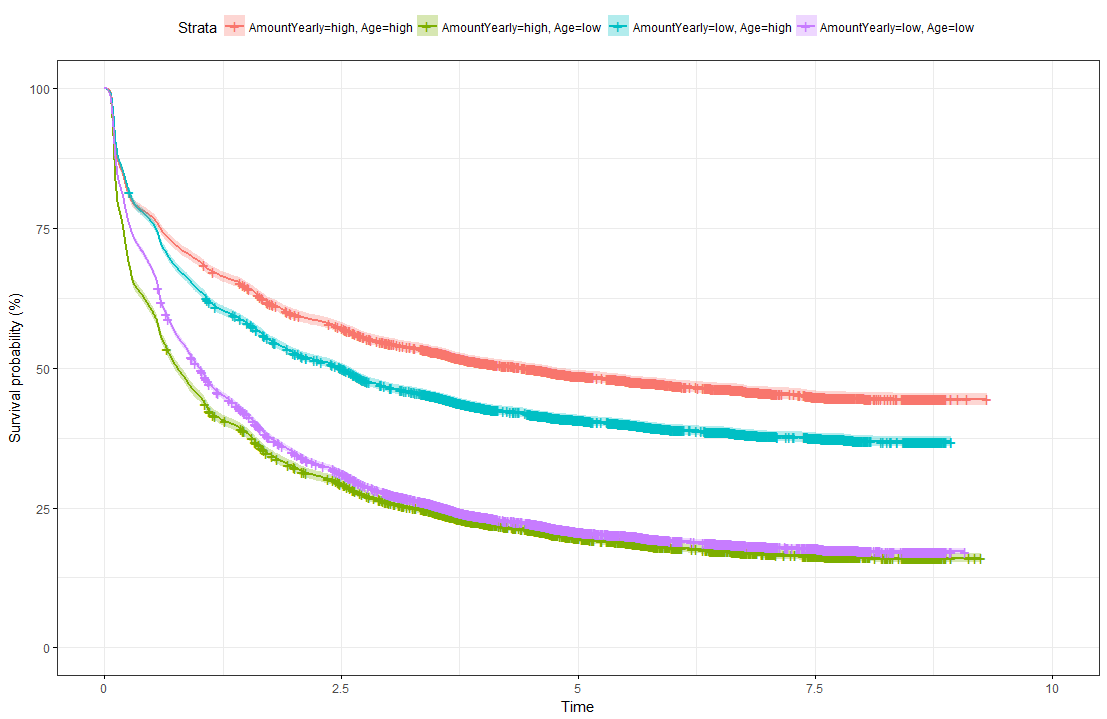
The illustration below shows Kaplan-Meier survival curves for different groups, the tick-marks on the curves represent censored observations. It can be observed that 50% of individuals terminate their commitment approximately within the first 1.5 years. We formed groups using using maximally selected rank statistics:  The groups exhibit different survival patterns:
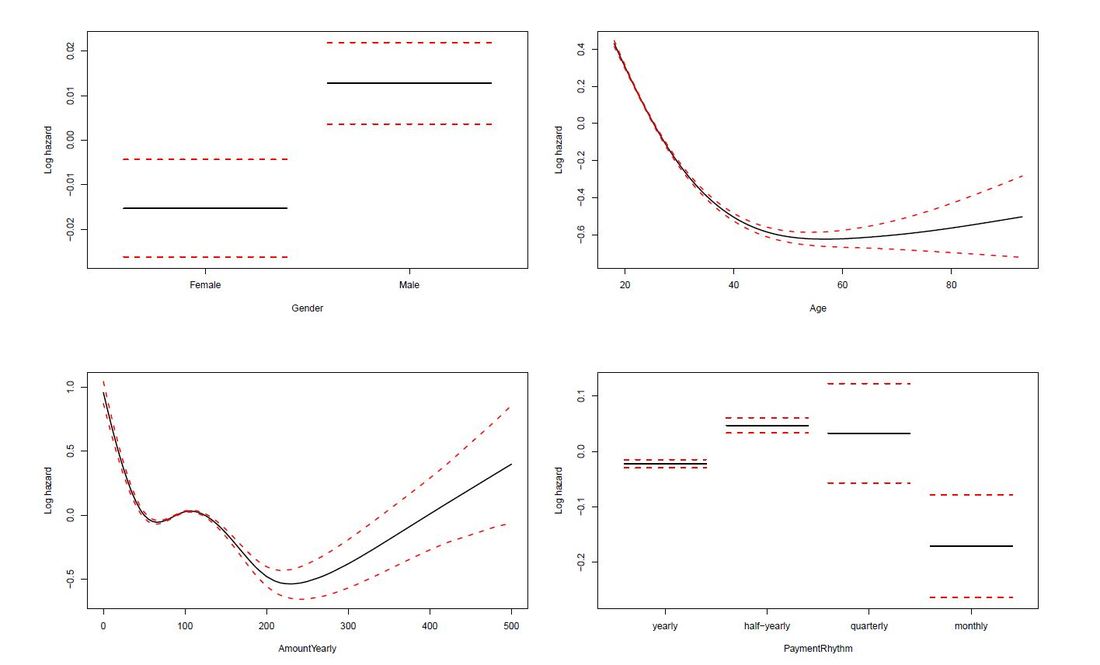
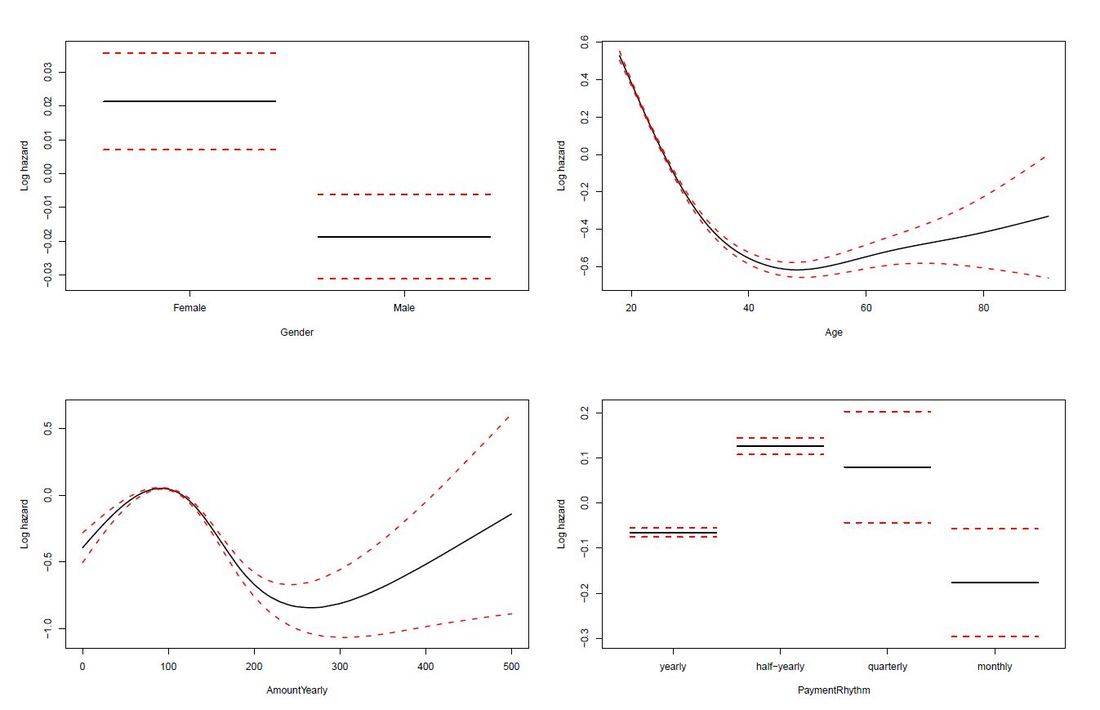
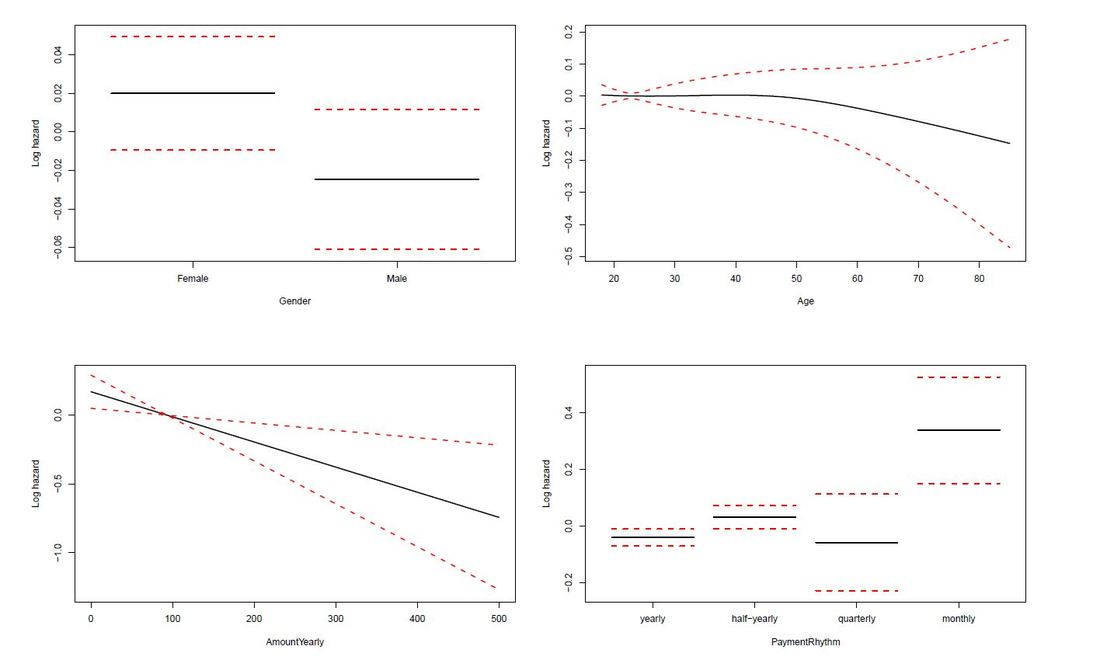
 Survival Curves splitted for different groups The limit of Kaplan-Meier curves is when several potential variables are available that we believe to contribute to survival. Thus, in a next step we employ a Cox regression model to be able to control statistically for several explanatory variables. Again, we are interested in whether the variables Age, Yearly amount payable, Gender, Payment Rhythm, and Region are related to survival, and if, in what manner. The relationship of Age as well as of Yearly amount payable on the log-hazard (the hazard here is the instantaneous risk - not probability - of attrition) is modelled with a penalized spline in order to account for potential nonlinearities. A Cox proportional hazard model First, we fit one Cox model for all data, including individuals who never started paying their commitments. The upper right panel in the figure below shows that the log hazard decreases (which means a lower relative risk of attrition) with rising age, with a slightly upward turn after age 60. But again, the data are rather sparse at older ages, which is reflected by the wide confidence interval and should thus be interpreted with caution. In the upper left panel, we see that the relative risk of attrition is higher for male than for female individuals. In addition, the lower left Panel depicts a non-linear relationship for the yearly amount payable, the log hazard decreasing the higher the yearly amount, (with a small upward peak at 100 Euro), and increasing again for yearly amounts higher than about 220 Euro (though data are again sparse for amounts higher than 200 Euro).  Termplot Cox-PH model (all observations) Include only individuals who started to donate... Next, we exclude individuals who never started to donate (i.e. those with a lifetime sum of zero) from the data, and then fit one Cox model for early data (with a commitment duration < 6 months) and one Cox model for later data (with a commitment duration > 6 months). Interestingly, some of the results undergo fundamental changes. ...and a commitment duration of > 6 months In the following, we present the termplots of a Cox model, including only individuals in the analysis who have a commitment duration of more than 6 months, and given the lifetime sum of the commitment is larger than zero. The gender effect turned the other way around compared to the model from the figure above. In addition, the shape of the non-linear effect of the yearly amount payable changed, if only the "later" data are considered.  Termplot Cox-PH model (commitment length > 6 months, lifetime sum > 0) ...and a commitment duration of <= 6 months Last not least the termplots of a further Cox model including only individuals with a commitment duration of less or equal than 6 months, and given the lifetime sum of the commitment is larger than zero are shown. Here, the age effect as well as the yearly amount payable do not seem to exhibit strong nonlinearities (actually, the effect of the yearly amount payable is linear). Furthermore, age does not seem to have an effect on the risk of attrition at all.  Termplot Cox-PH model (commitment length <= 6 months, lifetime sum > 0) Conclusion and outlook
1 Comment
|